Batch 2 - Class 272 - Ultimate tic tac toe
Zoom: send meeting Id and password
Start recording
Preclass Exercise:
- Arrange numbers 1-32 in a circle so that any two adjacent numbers sum to a square
- Answer:
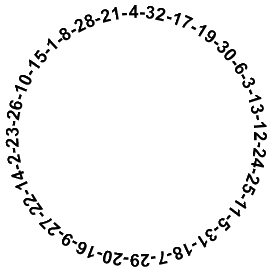
Attendance: Raghav, Aneesh, Kabir, Advay, Shikhar, Ayush, Vivaan, Rhea Chadha, Ryan Chadha, Rohan, Siddarth, Yatharth, Mihir, Dhriti, Aarushi, Akshita, Angad, Anika, Aarkin
Class Notes: (Repeat from class 152)
Ultimate Tic-Tac-Toe: Lay reference of standard tic-tac-toe and its deterministic nature. Let kids play a couple of games.
Introduce the ultimate tic-tac-toe, with following rules:
- Draw smaller tic-tac-toes in each square of larger tic-tac-toe
- Mark a smaller square on each turn
- When you get three in a row on a small board you win that small square
- To win the game, win three small boards in a row
- Next small board you play on is determined by which entry within previous smaller board your opponent played
- If you are directed to a small board which is already full, then you get to choose which board to play on
- If a small board is a tie, it neither counts as X nor O
Let kids play a few games.
Who wins the ultmate tic-tac-toe game? Is there a deterministic strategy?
Variation where if a small board is won, even if it is not full, the player being directed there can choose which board to play on. https://en.wikipedia.org/wiki/Ultimate_tic-tac-toe
Ultimate tic-tac-toe cannot be reasonably solved using any brute-force tactics. We can try computer programming to solve for this.
The most common artificial intelligence (AI) tactic, minimax, may be used to play ultimate tic-tac-toe, but has difficulty playing this. This is because, despite having relatively simple rules, ultimate tic-tac-toe lacks any simple heuristic evaluation function. This function is necessary in minimax, for it determines how good a specific position is. Although elementary evaluation functions can be made for ultimate tic-tac-toe by taking into account the number of local victories, these largely overlook positional advantage that is much harder to quantify. Without any efficient evaluation function, most typical computer implementations are weak, and therefore there are few computer opponents that can consistently outplay humans.
However, artificial intelligence algorithms that don't need evaluation functions, like the Monte Carlo tree-search algorithm, have no problem in playing this game. The Monte Carlo tree search relies on random simulations of games to determine how good a position is instead of a positional evaluation and is therefore able to accurately assess how good a current position is. Therefore, computer implementations using these algorithms tend to outperform minimax solutions and can consistently beat human opponents.
Homework Problem:
Rope around the world puzzle (Credit: William Whiston 1667-1752)
Take a tennis ball, and choose one of its equators. How much longer would you have to make the rope so that it is one foot from the surface of the tennis ball at all points?
What if we took the equator of earth. How much longer would we have to make the rope so that it is one foot from the surface of the earth at all points?
Let kids guess the answers to each.
Answer: In both cases the answer is about 6.28 ft (2 pi) - a surprising conclusion given that most people expect the earth answer to be much higher.
References:
The Math Book, Clifford A. Pickover